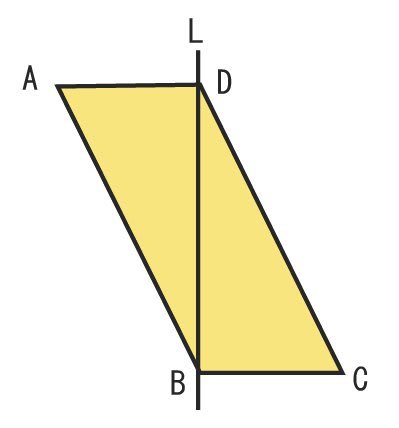
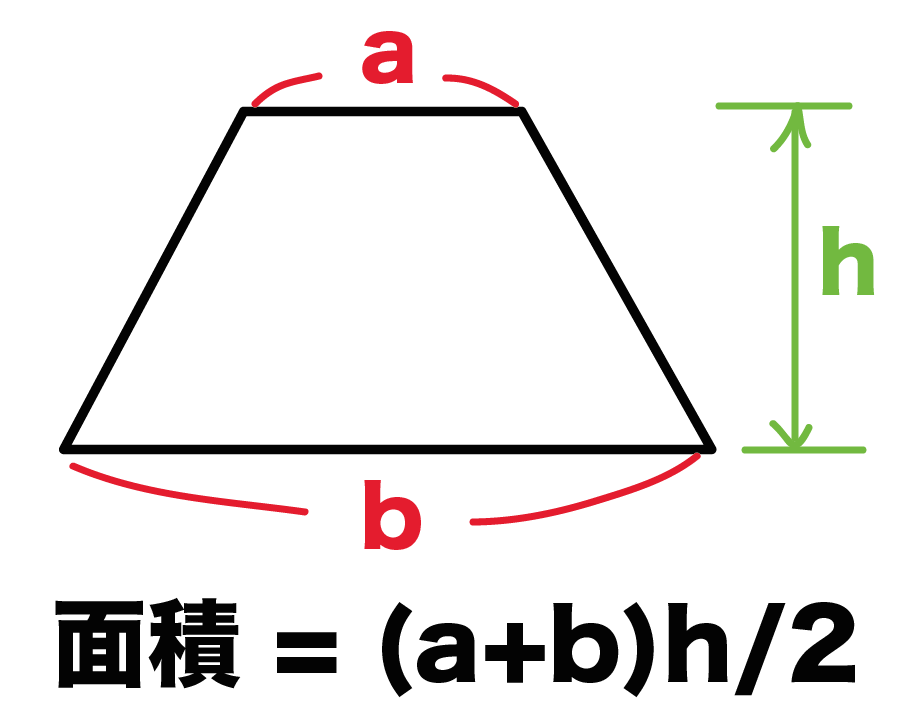
ここで定める"等積中心線"とは,台形内の底辺と平行な直線であって, それを中心として,台形面を面と垂直な方向に移動したときにできる上下のくさび形の立体の体積が等しくなる直線である (付図 3) . 台形の下底の長さを a ,上底の長さを b ,高
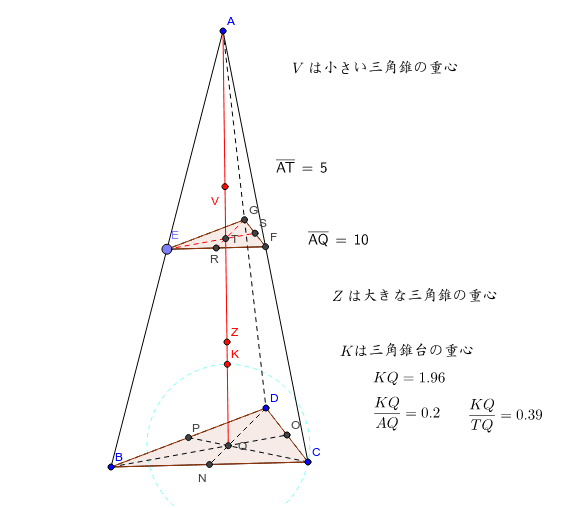
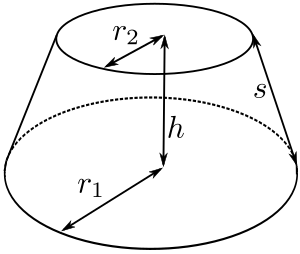
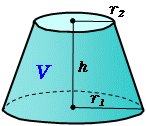
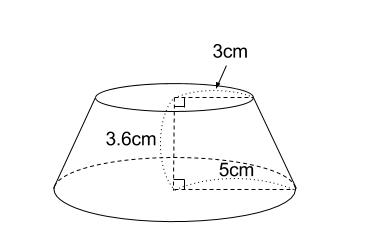
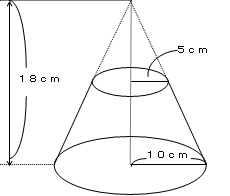
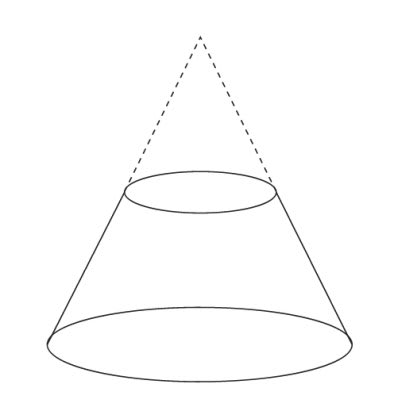
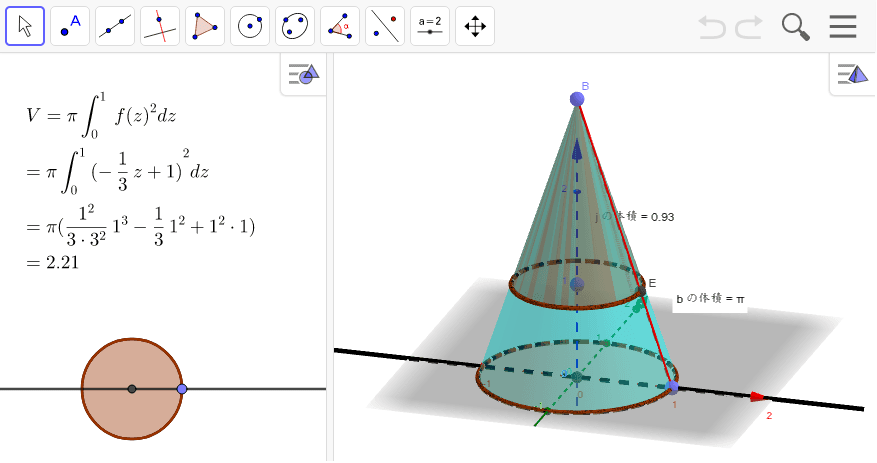
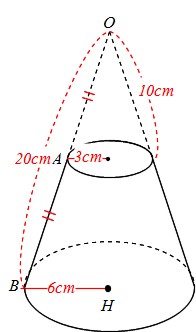
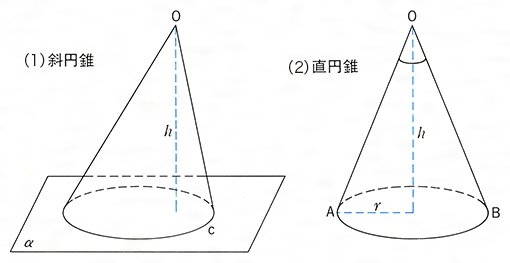
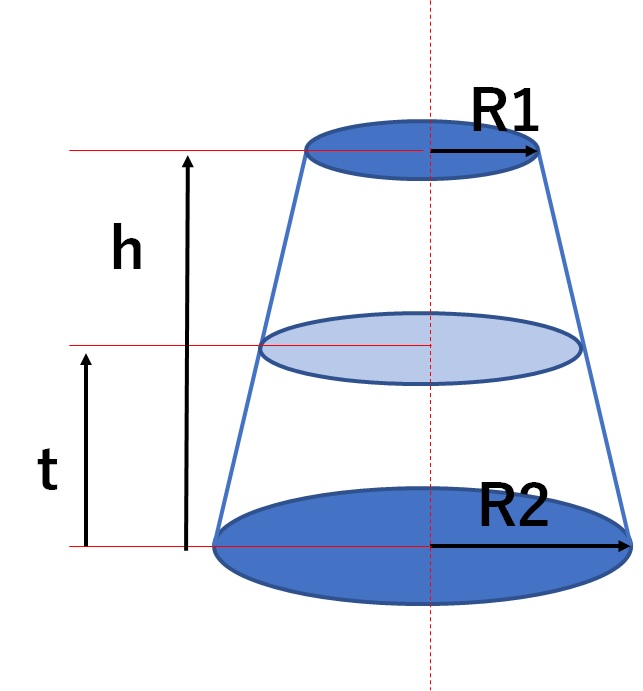
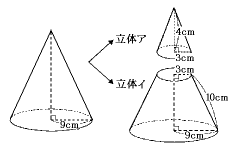
台形 円錐 体積- 積分 空間図形 積分 を用いて円錐の体積 V を求める以下の公式 を導出します. V = 1 3πr2h ここで, r は底面の半径, h は円錐の高さとします. 証明:まず,xy平面上に原点を通る直線を考えます.この直線とx軸とのなす角を θ とすると,この直線は y = (tanθ)x と表せます.この直線の式とx軸および2直線 x = 0 および x = h で囲まれた図形を,x軸の周りに1回転してできる立体 円錐台の体積 図1より、円錐台のもとになっている"大きな"円錐の高さは ah/(ab) 、底面の半径は a となります。 又、取り除かれる"小さな"円錐の高さは bh/(ab) 、底面の半径は b となり
台形 円錐 体積のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  |  |
 |  | |
 |  | |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  | |
 | ||
 |  | |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
 |  |  |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 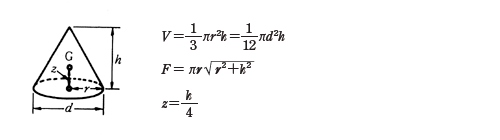 | |
 | ||
 |  |  |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  | |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 | ||
 |  |  |
 |  | |
 |  | |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 |  |  |
 | ||
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  | |
 |  |  |
「台形 円錐 体積」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |
メニューは、角、丸、三角、台形、六角、球、円錐、角錐です。 初心者でも簡単に入力が出来るよう解説図形を配置しました。 Figure Calculator 図形の面積・体積を一発計算します。 辺の長さなど入れるだけで面積、体積が求められます。さまざまな形状の面積、体積、重心位置、断面係数、慣性モーメントの計算を 行うことができます。 以下のように全部で34種類もの形状が準備されていますが、 試用できるのはその一部となっています。 「三角形、台形、長方形、箱形、四角形、箱形
Incoming Term: 台形 円錐 体積,




0 件のコメント:
コメントを投稿