Y=x2乗分の1 241066-Y=x2乗分の1

つまり， を2乗すると3になりますね。 では， を2乗してみると，どうなるでしょうか？ ここで，①，②より， と言えます。 この両辺の（ ）の中を比較して， となります。 一般に， と定義します。 例えば， ， です。 さらに，指数が， ではなく， の場合はどうなるかを考えましょう。 は，本当は， の2を省略して書いたものなのです。 つまり，3の 乗が と2乗すると必ずプラスになるので、 ただ、計算上そういう数があったほうが都合がよい、ということがあり、新たなルールとして「2乗すると－1になる数」を作り、それを「複素数」と呼んでいます。 高校で習うことがあるかもしれませんね。 まとめ（類題12－1の解答） (1) y = −log(C −ex) (2) y = Ce12x 2 (3) x2 y2 = C (4) y = log(ex C) (5) y =0;

3分の２乗の説明

Y=x2乗分の1

Y=x2乗分の1- 公式1： ∫ d x x 2 a 2 = log ⁡ (x x 2 a 2) \displaystyle\int \dfrac{dx}{\sqrt{x^2a^2}}=\log(x\sqrt{x^2a^2}) ∫ x 2 a 2 d x = lo g (x x 2 a 2 ) 公式2： ∫ x 2 a 2 d x = 1 2 ( x x 2 a 2 a 2 log ⁡ ( x x 2 a 2 ) ) \displaystyle\int \sqrt{x^2a^2}dx=\dfrac{1}{2}(x\sqrt{x^2a^2}a^2\log(x\sqrt{x^2a^2})) ∫ x 2 a 2 d x = 2 1 ( x x 2 a 2 a 2 lo g ( x x 21 y = − x2 2 C (6) y = x2 4 1!2 (7) y = Cx1 (8) y2 = C(2x− 1) (9) y =2x (10) y = e−cosx 例題12－2 dy dx = y xを解きなさい （例題12－2の解答） dy dx = yの解y = Cexp(x)を用いて,y = C(x)exp(x) とおいて, C(x)に関する微分方程式をつくる

Http Www Ikushin Co Jp Shuppan Textimg 16jack Chu3hyo Sugaku Hon Pdf

11年度数学I演習第11回 理II・III 17, 18, 19組 12 月15 日清野和彦 問題1 f を(0,0) 以外で定義された2 変数関数 f(x,y) = x2 −y2 (x2 y2)2とする。また、1より小さい二つの正実数a, b に対し有界閉集合Da,b を0,1×0,1 から0,a)×0,b) を取り除いたものとし、{a n}∞ =1と{bn}∞ を単調に減少して0 に極限計算機で関数の極限を計算します。片側、両側の極限もサポートされています。極限が計算されるポイントは、たとえばπ/ 4 のような数字または単純な式で指定することができます。極限の計算は正の無限大（ inf）、負の無限大（ minf微分の公式全59個を重要度つきで整理 具体例で学ぶ数学 > 微積分 > 微分の公式全59個を重要度つきで整理 最終更新日 このページでは、微分に関する公式を全て整理しました。 基本的な公式から、難しい公式まで59個記載しています。 重要度★★

ワードで2乗を入力する方法は？1分でわかる方法、上付き文字の表し方、数式の使い方 管理人おすすめ！セットで3割もお得！大好評の用語集と図解集のセット⇒ 建築構造がわかる基礎用語集＆図解集セット(※既に26人にお申込みいただきました！） ワードで2乗を入力する場合、「2オープニング（1分55秒） 円 x 2 ＋y 2 ＋lx＋my＋n＝0（5分38秒）;「yはxの2乗に比例」⇒y＝ax 2 中学1年生のときに学習した「比例」という言葉を覚えているかな？ yとxについて 「yはxに比例する」 という関係があるとき、その式は y＝ax（aは比例定数） と表せた

 x^2 の積分が (1/3) x^3 になるとは、 正方形を重ね合わせて作った立体の体積が、一辺 x の立方体の 1/3 になる、ということだ。 つまりこれは、四角錐の体積のことだ。 1つ次元を下げて、 x の積分が (1/2) x^2 になるとは、基本的な関数の微分 1 x 2 問題 次の関数の導関数を微分の公式および導関数の定義式を用いて求めよ． f (x) = 1 x 2 答 f ′ (x) = − 2 x 3 解説 f (x) = 1 x 2 = x − 2 と表すことができる． 公式を用いた計算 微分の公式を用いると， f ′ (x) = − 2 x − 2 − 1 = − 2 x − 3 = − 2 x 3 となる．中3数学。2乗に比例する関数（y ＝ ax²）の「変域」を求めなさい。うわ、変域って何？ 頂点が最小？ 分からん（ガクッ）倒れ込む中学生。立て、立つんだトォォォォ～ッ！ オール5家庭教師、見参ッ！ グイグイ成績が上がる数学のコツ。無料サイトだ。

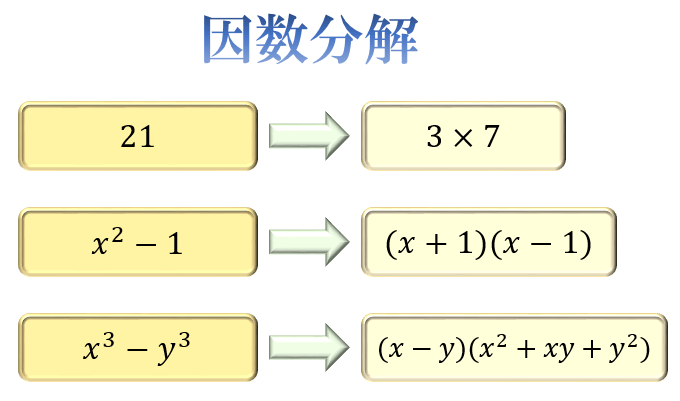
因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

X X分の一 3のとき X二乗 X二乗分の一 X四乗 X四乗分の一を求めよ Clear

例：y={(1/2)^x}1（2分の1のx乗プラス1） 使い方 式の入力には、数字と「x * / ( ) { }」を使用します。すべて半角です。 ×は「*」、÷は「/」を用います。 絶対値記号やガウス記号を使用することもできます。べき乗は、{底^指数}で表現します。 例：y=x, y=x, y={2^x}ただし、2乗の場合は squared 、3乗の場合は cubed が用いられます。 $ 10^2 $ ten squared $ 2^3 $ two cubed 累乗の底を base 、指数を exponent といいます。 根号（ルート） radical sign 根号を英語で読むには、"the nth root of ~" の形で読みます。 $ \sqrt4{7} $ the forth root of seven ただし、平方根は "the square root of三角比の微分は、必ずこの形を覚えておきましょう。 ( \sin x)' = \cos x (\cos x)'=\sin x (\tan x)'=\frac {1} {\cos^2 x} また、場合によってはこれらの変形も必要になってくるので覚えておきましょう。 \sin^2 x=1\cos^2 x \cos^2 x=1\sin^2 x \tan^2 x=\frac {\sin^2 x} {\cos^2 x

Y 3分の1ｘ2乗 2ｘのグラフの ｘ切片の求め方を教えて下さい Y 0のときの途中 Clear

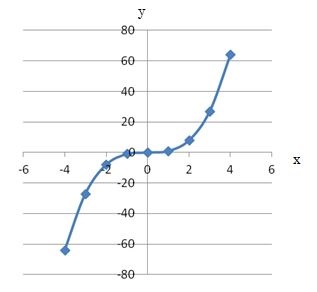
3次関数 方程式 のグラフ もう一度やり直しの算数 数学

 一般に、指数関数 y = ax y = a x について、 x = 0,1 x = 0, 1 のときに y = 1,a y = 1, a であることから、グラフは、 (0,1) ( 0, 1), (1,a) ( 1, a) の2点を通ることがわかります。 また、 x x が1増えれば y y は a a 倍に、1減れば 1 a 1 a 倍になることから、 a > 1 a > 1 ならグラフは2乗のものを2乗のもので引いた式は、和と差の積に変換できるのが因数分解の公式3です。文字の2乗はわかりやすいですが、気をつけたいのは数字の2乗です。数字は平方根が整数になるかを確認する必要があります。 x 216 16は4 2 なのゼロ乗・マイナス乗・分数乗・無理数乗ってどういう意味？ 23 や 34 に限らず、 3 − 2 ・ 51 2 ・ 8 π といった値も含めた「 a の n 乗」の形で表される数 an のことを 「a のべき乗」 と言います。 この記事では、べき乗の定義と「 3 − 2 ・ 51 2 ・ 8 π とは具体

Y 1 X2乗のグラフ Youtube

２次関数のグラフ

部分積分法 より． f ′ (x) = 1, g(x) = √a2 x2 f ′ ( x) = 1, g ( x) = √ a 2 − x 2 = x√a2 x2 − ∫a2 x2 − a2 √a2 x2 dx = x √ a 2 − x 2 − ∫ a 2 − x 2 − a 2 √ a 2 − x 2 d x = x√a2 x2 − ∫√a2 x2dx ∫ a2 √a2 x2dx = x √ a 2 − x 2 − ∫ √ a 2 − x 2 d x ∫ a 2 √ a 2 − x 2 d x = x√a2 − x2X2y′ = (x − 1)y の一般解を求めよ 解答 この方程式は形式的に dy y = „ 1 x − 1 x2 « dx と書けるので変数分離形である 従って両辺を積分して より また も解なので も含めて最終的な答えは は任意の定数 I 常微分方程式– p6/31A x の微分法 a x をxで微分するとどうなるか考えてみよう。 まずは、底の変換をして、微分することをやってみよう。 いいかな。結果は覚えておこう。 つぎに、両辺の対数をとる方法。

X 1分のx2乗 X分の1の解き方を教えてください ただの通分 Yahoo 知恵袋

3

(1) y = x 2 x1 考え方 x 2 の微分は 2x x の微分は 1 1 の微分は 0 これらを加えると y' = 2x1 (2) y = 5x 6 −3x 2 考え方 x 6 の微分は 6x 5 だから 5x 6 の微分は 30x 5 x 2 の微分は 2x だから 3x 2 の微分は 6x これらを引くと y' = 30x 5 −6x よって、 ∫x^ (a1)dx＝ (1/a)*x^a＋C →∫x^adx＝ {1/ (a1)}*x^ (a1)＋C となります。 つまり、 ∫1/x^2 dx＝∫x^ (2)dx ＝ {1/ (21)}*x^ (21)＋C ＝－x^ (1)＋C ＝－1／x＋C数学 中学生 1年以上前 あんころもち y=1/2x^2 (二分の一エックスの二乗)のグラフを書いてみたのですが、これでいいのでしょうか グラフに点を取るときに、偶数を当てはめたんですが (a=1/2のため)、そうすると点は2と4 (2と4)しかとれません xが4以上

Yx2乗 ニスヌーピー 壁紙

Yx2乗 ニスヌーピー 壁紙

カイ2乗分布（グラフ） 12 /2件 表示件数 5 10 30 50 100 0 1 1547 男 / 40歳代 / 教師・研究員 / 役に立った / 使用目的 自由度の大きさに応じてカイ自乗分布の形がどのように変化していくかを初学者に示す際に役立った 2 1627 女 / 50歳代1 積分練習問題解答 1 つぎの不定積分を計算せよ。 (1) ∫ x 1 x2 2x5 dx d dx (x2 2x5) = 2(x1)だから x 1 x2 2x5 x1 x2 2x5 2 x2 2x5 と変形して，y = x2 2x5 とおくとdy = 2(x1)dx だから ∫ x1 x2 2x5 dx = ∫ dy 2y = logjyjC = 1 2 log(x2 2x5)C一方，後半の積分はx 22x5 = (x1) 4 なので，y = (x1)/2 と書くと陰関数の微分法 y=2x1 のように y について解かれた形になっているものを陽関数， x 2 y 2 =1 のように x ， y の関係式で示され， y について解かれた形になっていないものを陰関数という． 陰関数で表わされているものを微分するには，右の例のように両辺をそのまま微分すればよい．

この2問の解き方を教えてください 答えは 5 が 6 が です Clear

高校数学 Y Ax 2 Bx Cのグラフ 例題編 映像授業のtry It トライイット

 xのn乗の微分公式 (xn) ′ = nxn − 1 ( n は 実数 ) 最も基本となる公式 (1 x) ′ = − 1 x2 (√x) ′ = 1 2√x (xn) ′ = nxn − 1 に n = − 1 や n = 1 2 を代入すると求まる  1606 tan (x)の逆関数arctan (x)の微分を考えます。 y=arctan (x)の微分 x=tan (y) dx/dy=1/cos^2 (y)=1tan^2 (y) (∵三角比の相互関係)x=tan (y)だから 1tan^2 (y)=1x^2 つまり dx/dy=1x^2となったわけです 逆関数の微分法 dy/dx=1÷dx/dy=1/ (1x^2) つまりy=arctan (x)をxで微分すると1/ (1x^2)ということです 従って ∫dx/ (1x^2)=arctan (x)C ナイス！・y=g(x)=x 2 の極限の性質より、 y=g(x)= x 2 は、 どんな実数aに対しても、 g(x) →a 2 (x→a)。 ・「関数どおしの積」の極限は、「関数の極限」どおしの積となるという定理と、 上記で得られた

Xの二乗 Xの二乗分の1は X X分の1 の二乗プラス2x っ Yahoo 知恵袋

二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い

5分で解ける！カッコ×カッコの公式2 (x＋a)^2，(x－a)^2に関する問題 67 子どもの勉強から大人の学び直しまで ハイクオリティーな授業が見放題 この動画の問題と解説 練習 一緒に解いてみよう 解説 これでわかる！ 練習の解説授業 （x＋a） 2 や（x－a） 2 の公式を使って解く問題だね。 公式文献 ・『岩波数学入門辞典』平方根(p543) ・吉田栗田戸田『高等学校数学I』(p53) 上記2文献では、「R＝(－∞,∞） で定義された1変数関数 y=f (x)= x 2 」による実数yの逆像を平方根と呼び、 実数y>0のとき、二つある平方根のうち、正のほうを√yで表すとしている。Y=2x 2 上の任意の点を (x,y) ，平行移動を行なった後の点を (X,Y) とします。すると， X=x2，Y=y1 となります。よって，古い座標を新しい座標で表すと， x=X2，y=Y1 となり，この関係式を y=2x 2 へ代入すると， Y1=2(X2) 2

この関数のグラフを描きたいのですが 曲線の式は X 2 Y 3 Okwave

3分の２乗の説明

 次の二次関数の最大値、最小値を調べよ。y=X二乗－2X－3 （0≦X≧3）の解き方を教えてください。y=x²2x3 ①二次関数の最大値、最小値のときは、そのグラフを描き、xの範囲と頂点を調べます。①のグラフは 下に凸で、 頂点は(1,4) ∵y というわけで、 まずは接点を求めていきましょう。 微分した式が になるところ、それが今回の接点の 座標となります。 座標が分かれば、 に代入することで 座標も求めることができます。 、よって接点は 。 、よって接点は 。 このように2つの接点を求めることができました。 これで接点と傾きが揃ったので、 接線の方程式を作っていくことができます定積分の計算には，そのうちどれか1つの原始関数を用いればよいが，計算が簡単なように C=0 となるものを用いる． すなわち， n F (x) C = (F (b) C )− (F (a) C )=F (b)−F (a) となり，どんな C の値を用いても差で消えるので，計算が最も簡単になる C= 0 の場合を

この2分の1はなぜx2乗 Y2乗 Z2乗にもかけられるのですか X Yahoo 知恵袋

2次関数 中学 三角形の面積を二等分する直線の式 勉強ナビゲーター

平方完成の手順 平方完成は以下の手順で行うとよい。 ① x を含む項だけ、 x2 の係数でくくる ② x の係数を半分にして、2乗を足し引きする ③ 因数分解する ④ 分配法則を用いる ⑤ 定数項を計算する 例えば、3 x2 12 x 6を平方完成すると、 となる。積分電卓 積分する関数を入力してください 変数 被積分関数 1/ (x^41) を次の変数で微分する x (log (x1)2*atan (x)log (x1))/4 注意 log 自然対数 グラフを描く LaTeXエディタで編集 このページへの直接のリンク 変数に次の値を代入する x= 積分電卓 解析積分式、値の変化、グラフなどから関数関係を分析し、その特徴を理解し、問題を関数的に解決する y = ax2 y = a x 2 の関係にある数量を、表、式で表したり、変数の変域、変化の割合を求めたり、曲線上の2点を通る直線の式を求めることができる 関数 y = ax2 y = a x 2 ・変化の割合の意味，関数 y = ax2 y = a x 2 のグラフの特徴，直線の式の求め方を理解する

因数分解とグラフ 中学から数学だいすき

数学 中3 35 二次関数のグラフ Youtube

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

3分の２乗の説明

2 の問題を教えて下さい 何で最後にx2乗を引いてるんですか 2 高校 教えて Goo

3年 関数 Y X のグラフ 数学イメージ動画集 大日本図書

2次関数の問題で Y X２乗 X 1のグラフがこうなるのは何故ですか Yahoo 知恵袋

これがわかりません Clear

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

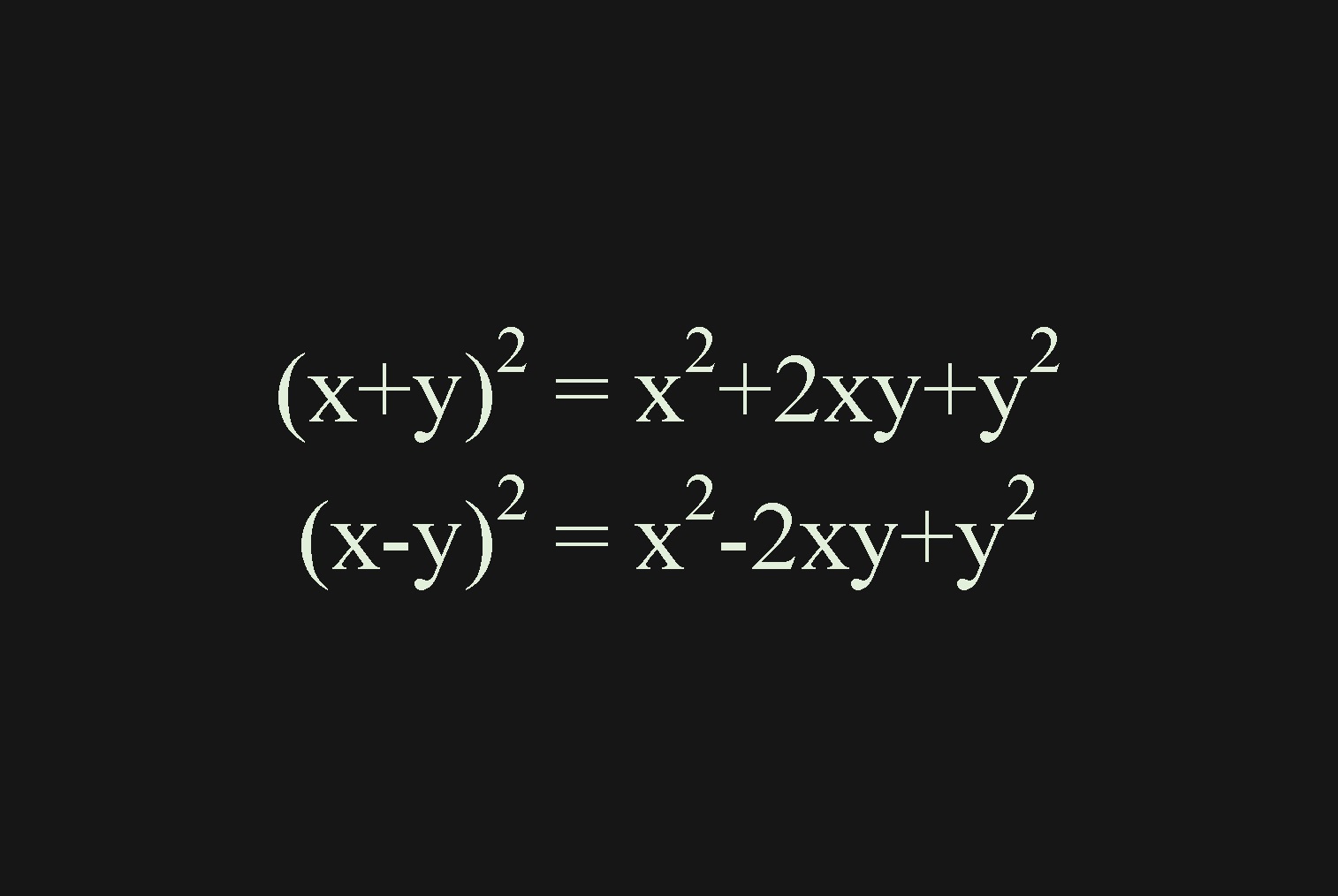
分数を指数とする累乗 1 2乗の意味 統計学が わかった

X2乗 1分の3x 5 X2乗 X分の1の解き方を教えてください こ Yahoo 知恵袋

Eの2x乗の微分や積分は Eの3x乗の微分や積分は Eのマイナスx乗の微分や積分は E 2x E 3x E X ウルトラフリーダム

3分の２乗の説明

Http Www Ikushin Co Jp Shuppan Textimg 16jack Chu3hyo Sugaku Hon Pdf

Xの二乗分の1 ｙの2乗分の一を通分するとなぜxの2乗ｙの2乗分のxの二乗 Yahoo 知恵袋

数学の質問です 分数関数の分母に二乗がついていた場合はどのように計 数学 教えて Goo

Yx2乗 1 ニスヌーピー 壁紙

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

なぜ4のx乗分の1が2分の1のx乗の2乗になって Clear

Y 1 X2乗のグラフ Youtube

Mathematics 関数と証明 大阪府公立 ２２年前期理数科 働きアリ

1 12公式 3次関数 おいしい数学

数学です Y 1 X 2のグラフで X 2のときは X 2に近づくと無限大に発散す 数学 教えて Goo

Y 3分の1xの2乗の関数のグラフはどのようにしてかけばいいの Yahoo 知恵袋

高校数学 因数分解 3乗が登場する因数分解の解き方をわかりやすく解説 数学の面白いこと 役に立つことをまとめたサイト

X 1分のx X2乗 2x 3分の3x 1の解き方を教えてください Yahoo 知恵袋

Yx2乗 ニスヌーピー 壁紙

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

高校数学 2次関数がx軸から切り取る線分の長さ 受験の月

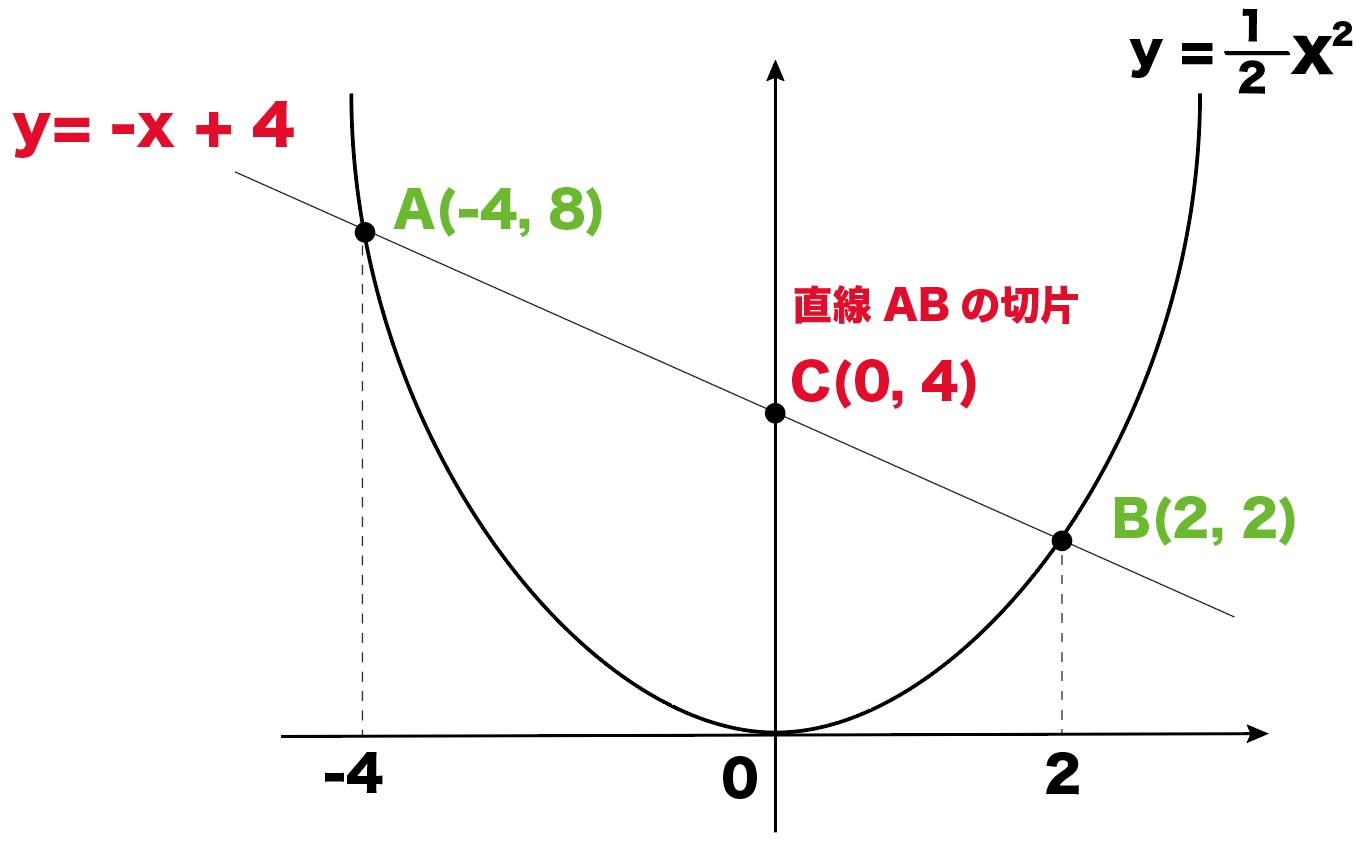
二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく

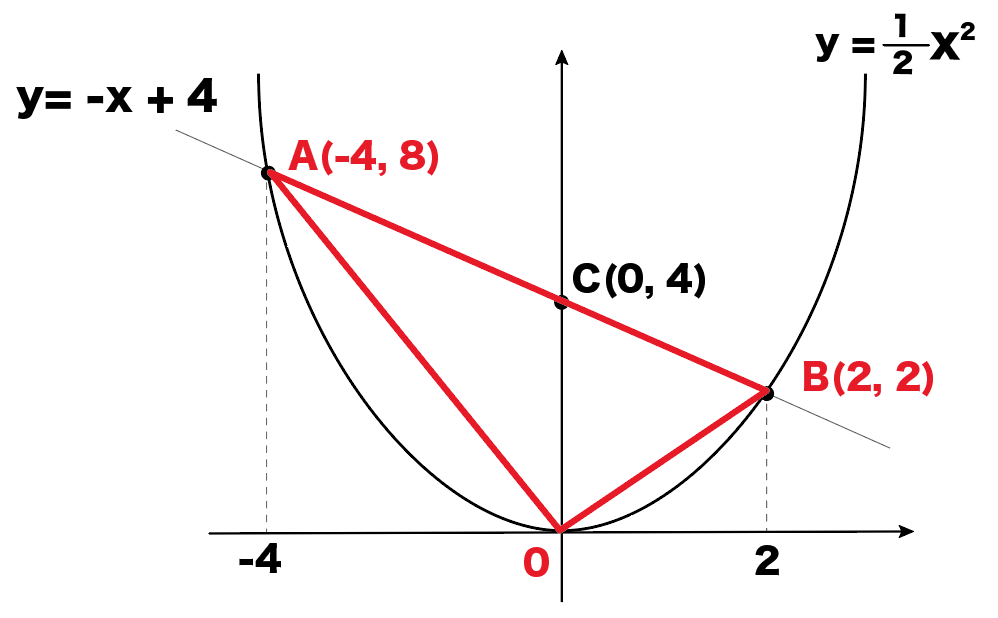
二次関数のグラフで三角形の面積を求める問題の解き方4ステップ Qikeru 学びを楽しくわかりやすく

４乗のグラフ ２乗のグラフは学校で習いました ４乗のグラフはどんな 数学 教えて Goo

2次関数のｙ ２分の１ｘ２乗の票の作り方を教えて下さい 2次 Yahoo 知恵袋

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

積分の面積公式と証明 6分の1公式 接線など 理系ラボ

Ftp Ftp Hp Com Pub Calculators Prime Documentation Calculator Jpn User Guide Jpn 15 06 17 1 Pdf

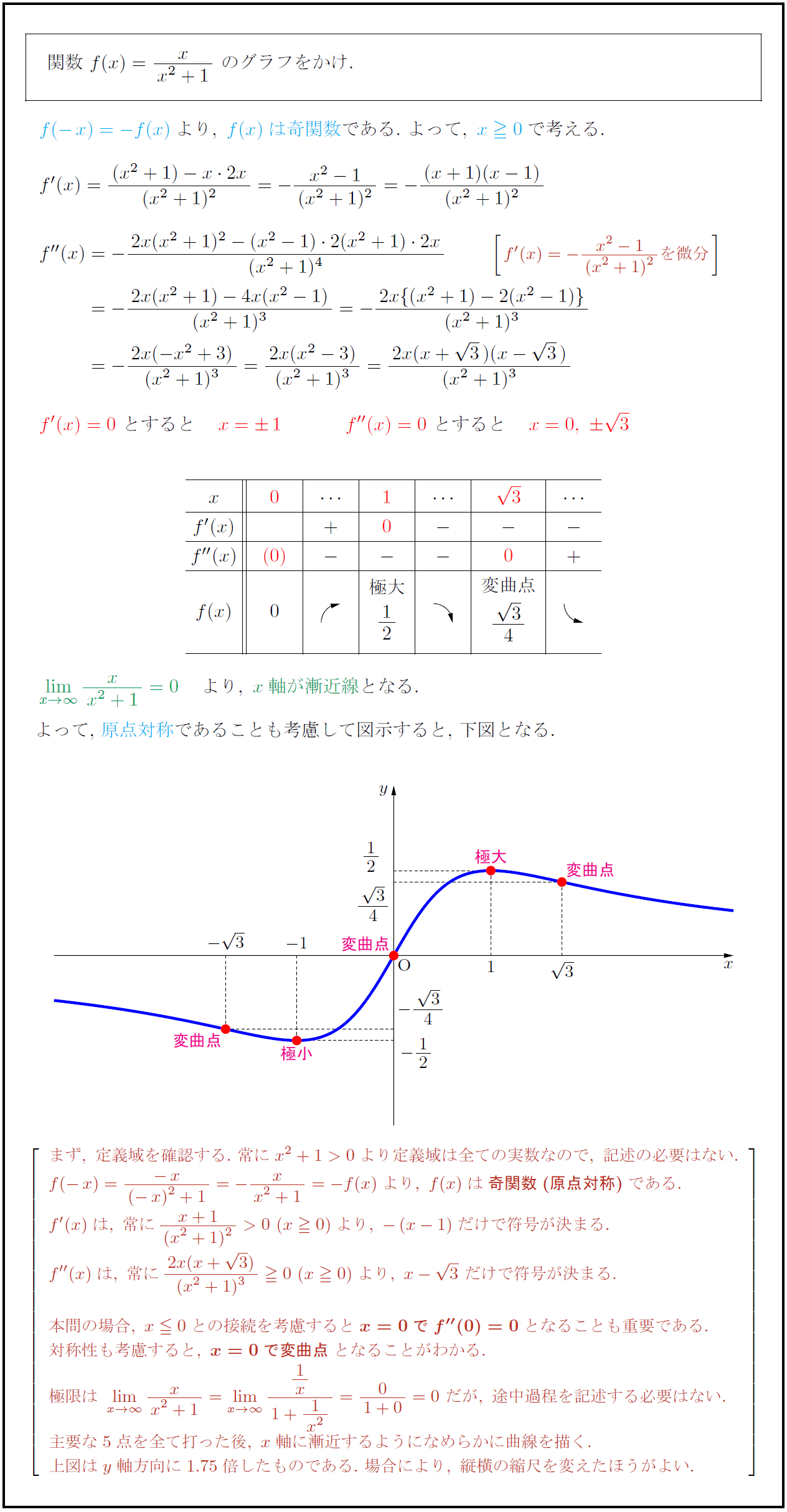
高校数学 分数関数 Y X X 1 のグラフ 受験の月

６分の１ １２分の１ ３分の１ A Day In Our Life

二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

Y X2乗 4の式で頂点と軸を求めてグラフを書けと言われました答えはわかるの Yahoo 知恵袋

Xの2乗 Xの2乗分の1 7の時t X X分の1とおくとtの2乗 Yahoo 知恵袋

２次不等式の解き方 X 4x 5 0 X 4x 5 0の形をした問題 数学i By ふぇるまー マナペディア

因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

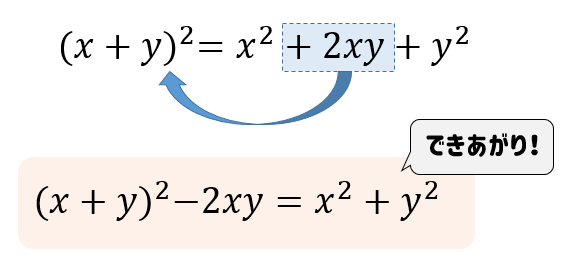
二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

二次関数グラフの書き方 頂点を一発で求める方法とは 高校生向け受験応援メディア 受験のミカタ

1

Y ｘ二乗 ｘの微分を教えてください Peing 質問箱

X二乗 ｙ 三乗根 ２二乗 二乗 １ 恋愛グラフへのボケ ボケて Bokete

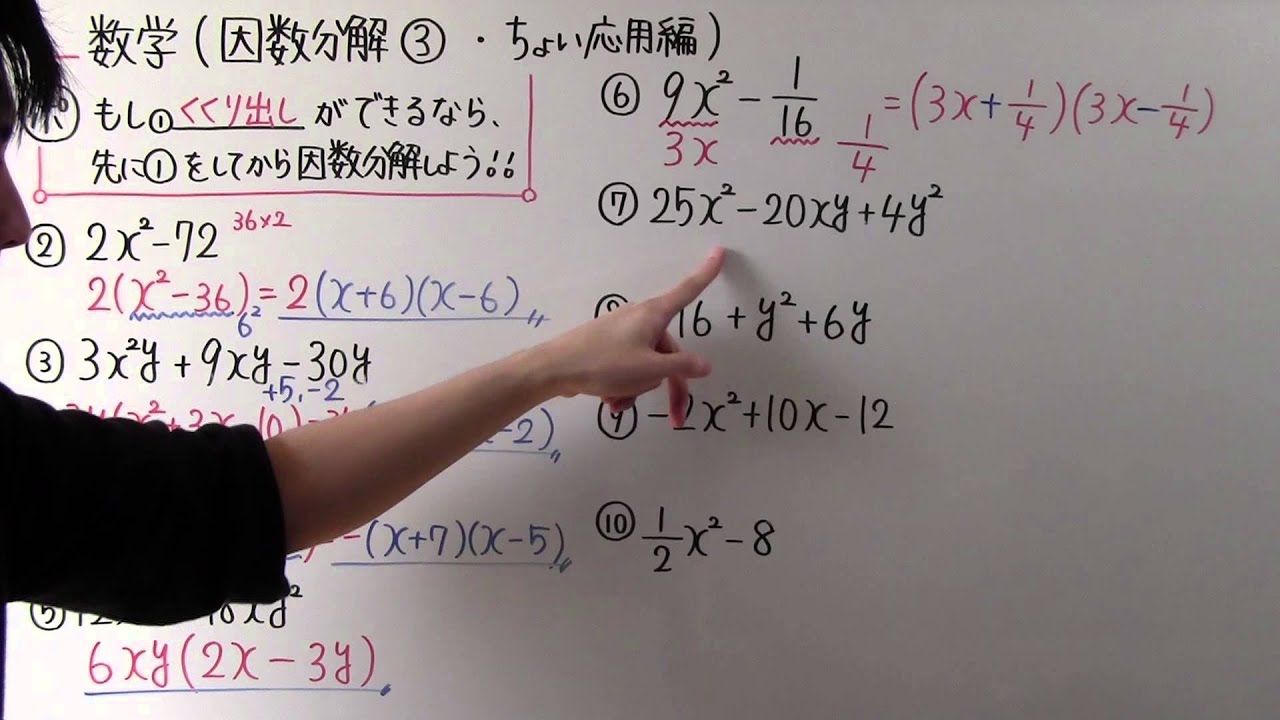
数学 中3 8 因数分解 ちょい応用編 Youtube

高校数学 対称式 この問題の 3 の解き方が分かりません 途中式も含め Okwave

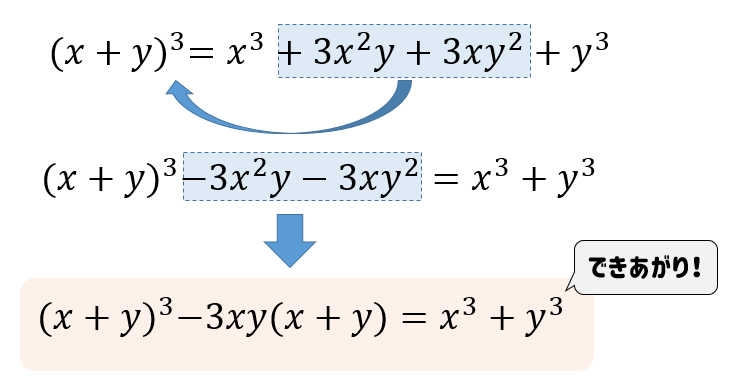
二乗足す二乗の公式 なんでこんな変形になる どんな場面で活用する 数スタ

中3数学 Y X2乗とy X2乗のグラフ 5分で学習 Youtube

指数 対数関数 ２分の１乗の意味 数学 定期テスト対策サイト

Y Xの二乗 1 のグラフを書いてくれませんか Yahoo 知恵袋

Y Xの2乗分のx2乗 1の式を微分してグラフを書く問題があります Yahoo 知恵袋

中3数学 Y 2分の1x2乗のグラフと変域 5分で学習 Youtube

1

Yx2乗 1 ニスヌーピー 壁紙

数学小話 いろいろ拡張しよう マイナス2分の1乗とは 日比谷高校のススメ

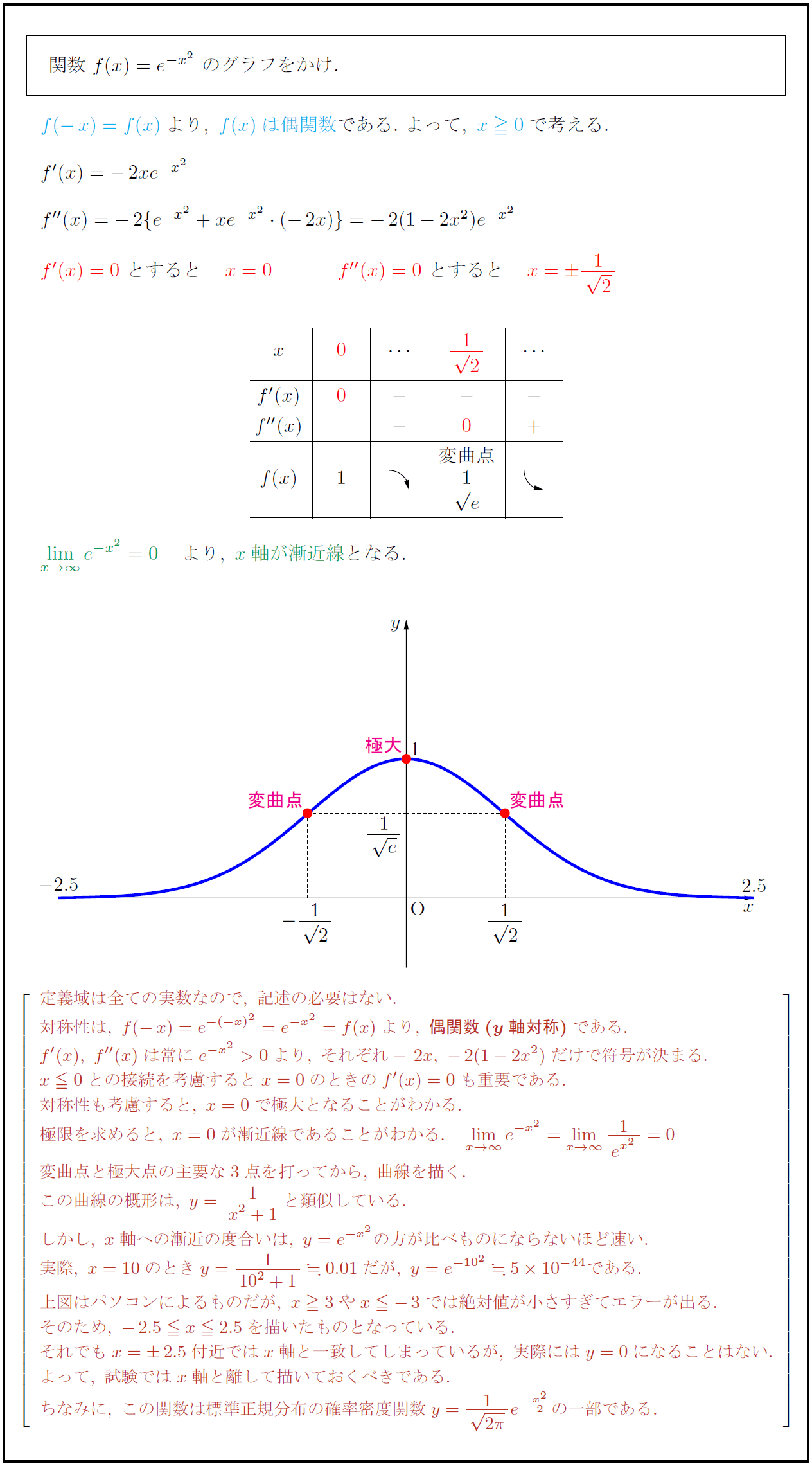
高校数学 指数関数 Y E X のグラフ 正規分布曲線もどき 受験の月

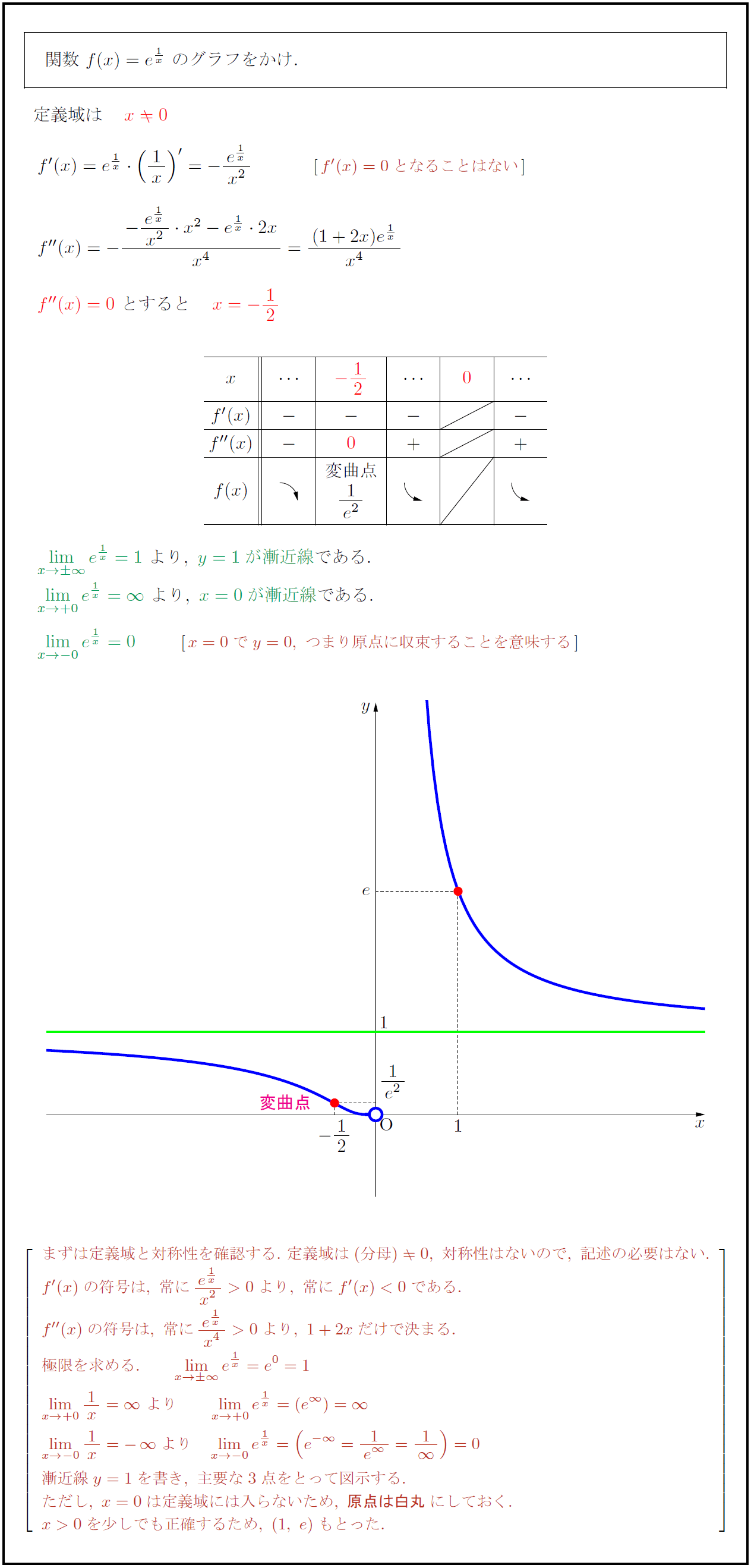
高校数学 指数関数 Y E 1 X のグラフ 受験の月

中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

数学小話 いろいろ拡張しよう マイナス2分の1乗とは 日比谷高校のススメ

関数y Ax2乗 放物線グラフの書き方はこれでバッチリ 数スタ

中3数学 Y X2乗のグラフ 5分で学習 Youtube

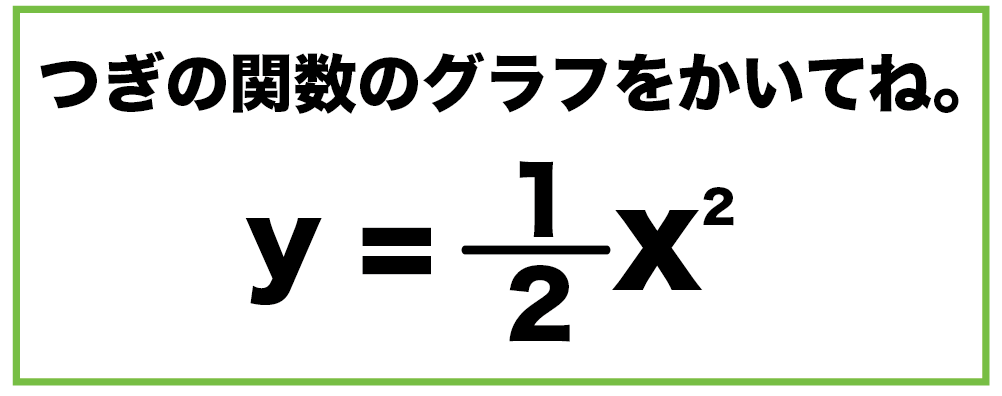
中学数学 二次関数y Ax2のグラフの書き方がわかる3つのステップ Qikeru 学びを楽しくわかりやすく

中3数学 Yはxの2乗に比例 とは 映像授業のtry It トライイット

中学数学 1次関数と2次関数y Ax2のグラフの3つの違い Qikeru 学びを楽しくわかりやすく

二乗に比例とは 1分でわかる意味 式 グラフ 例 比例との違い

2 裏業

第２種スターリング数を観察する ９ 降階乗の和分と R 乗和の公式 怜悧玲瓏 高校数学を天空から俯瞰する

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

Q Tbn And9gctfwtlkzxtbj Qqh8hpisvji7cqnwn Wo7yrdkltvorzjrkuks4 Usqp Cau

これがわかりません Clear

Y 1 X ２乗 4 写真が分かりやすいと思います の増減 凹凸な Y 1 数学 教えて Goo

偏微分の意味とやり方

中学校数学 3年生 数量 2乗に比例する関数 Wikibooks

数学 計算 X二乗 Xy Y二乗 X二乗 Xy Y二乗 X4乗 X二乗y二乗 数学 教えて Goo

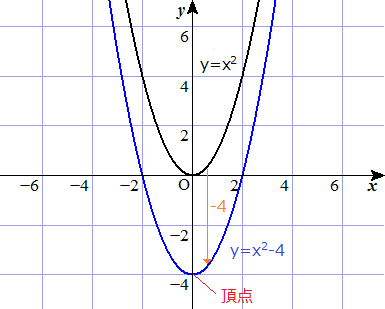
例題で学ぶ高校数学 Y Ax2 Q

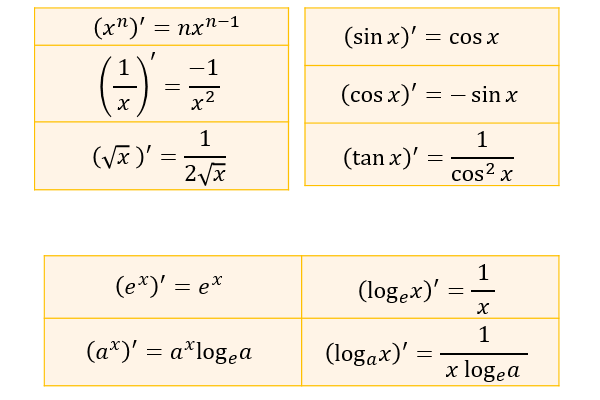
因数分解の問題の解き方とコツ 2乗 3乗公式とたすきがけ アタリマエ

Http Www Edu City Fukuyama Hiroshima Jp Chu Johoku Revolution Actionplan Syutaiteki Manabi01 6 Shidouan K29 07m Pdf

基本 二次関数y A X P 2のグラフ なかけんの数学ノート

2 の問題です Xの4乗 4を因数分解するという問題なのですが 2行 高校 教えて Goo

X X分の一 3のとき X二乗 X二乗分の一 X四乗 X四乗分の一を求めよ Clear

２乗に比例するグラフ 中学から数学だいすき

Incoming Term: y=x2乗分の1,